The Fractals' Math
How can Fractals be generated? And what's their characteristics?
How can they be generated?
Fractals can be generated by:
- computer
- mathematical formulae
- iterations
- rendering algorithms
The most important feature of a Fractal are iterations. To obtain spectacular result, a high number of iterations must be computed. This number can be infinite too.
Unfortunately, computers don't have unlimited computational capacity. If the number of iteration are high enough, flaws are not visibile by human eye anymore.
These imperfections remain hidden whether the Fractal is magnified. However, if the zoom is too high, these flaws are visible again.
To overcome this problem, the Fractal must be generated with increased number of iterations. Nevertheless, the computation will become more and more complex, therefore it will become slow.
Iteration
Iteration is a single computation applied recursively on a formula. A recursion is the calculation of a function which uses previous results as parameters.
For instance, we compute this formula:
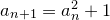
If we set 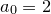 , then the first iteration is:
, then the first iteration is:
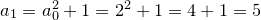
The second iteration is:
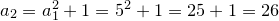
The third iteration is:
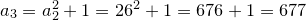
And so on.
Complex Fractals can be rendered with simple mathematical computation. However, complex rendering algorithms are required to generate and view these Fractals correctly and efficiently.
Fractals' rendering algorithms
Rendering algorithms classify each Fractal by a particular set. The most important Fractals sets are:
- Lindenmayer system Fractals
- Escape time (or orbit) Fractals
- Flame Fractals
- Chaotic attractors
- Three and four dimensional Fractals
- And more
The simpliest Fractal are generated by Lindenmayer algorithm. For each iteration, this algorithm transform every side to a repeated geometric structure.
The starting geometric shape is axiom. Rule states how each side must be repeated.
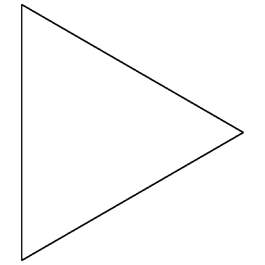
For example, we take the Von Koch snowflake. The axiom is:
The rule of a single side is:
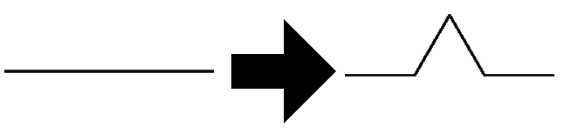
The axiom is a triangle with three equal sides. This rule transform each side into a four sided shape. If we apply this rule for each side on the axiom, the shape will become a twelve sided star. Therefore, the transformed shape is the Von Koch snowflake at first iteration:

The second iteration transform the shape into
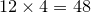 sided one:
sided one:
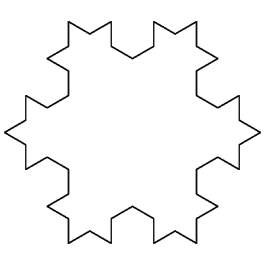
The third iteration transform the shape into 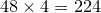 sided one:
sided one:
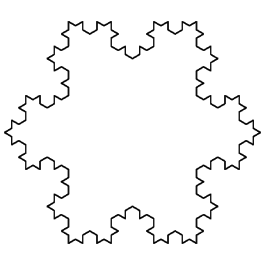
After a suffient number of iterations, the shape will be like a real snowflake:

It should be noted that this Fractal doesn't have got any visibile flaws, thanks to a high enough number of iterations.
Conclusion
Fractals can copy natural shapes, such as snowflakes, trees, plants (for example cauliflowers) and so on. These algorithms can also be used to render realistic natural environment, with little human efforts.
